Chen Wei, Yu Zhou, Lihua Jin*
Department of Mechanical & Aerospace Engineering, University of California, Los Angeles
*Corresponding author: lihuajin@seas.ucla.edu
Introduction
Liquid crystal elastomers (LCEs) are special elastomers with a combination of cross-linked elastomers and rod-like liquid crystals (LCs), thereby exhibiting both the hyperelasticity of elastomers and the unique properties associated with LCs[1]. LCs align in certain direction, called the director. On one hand, mechanical deformation not parallel to the director can reorient the director to the loading direction, inducing a stress plateau in the stress-strain relationship[1], [2]. On the one hand, LCs can rotate under various external stimuli, such as heating, light irradiation, magnetic fields, and electrical fields, leading to macroscopic spontaneous deformation[3].
In this particular journal club, we will mainly focus on recent work about mechanical behavior of LCEs. The discussion will be divided into three key sections. Firstly, we will examine the rate-dependent behavior of stress, strain and director under varying uniaxial loading rates, alongside several newly developed viscoelastic models. Secondly, we will explore the unique coupling between stress and director in LCEs, which results in anomalous inhomogeneous deformations that differ significantly from those observed in traditional elastomers. Finally, we will discuss how the stress-director coupling leads to distinct fracture characteristics. Our study will focus on nematic main-chain monodomain LCEs, where the LC mesogens tend to align in a specific orientation, i.e. the director, which can be identified by their uniaxial optical axis.
Viscoelastic constitutive behavior
Significantly rate-dependent stress-strain relations and extremely slow shape recovery have been reported in LCEs[4], [5], [6]. Due to the complicated synergy of the network and LCs, we show not only rate-dependent stress, but also rate-dependent director rotation as well as shear strain components. Following the methodologies of Mistry et al.[7] and Blaber et al.[8], we employed optical polarization and digital image correlation (DIC) to capture the rate-dependent stress, strain and director at varying uniaxial tension (Figure 1a)[9]. By comparing the stress and director values in uniaxial tension and relaxation tests, we find that the characteristic relaxation time of the network extension is significantly larger than that of the director rotation. The director almost reaches equilibrium at a loading rate around 1%/s, while stress does not reach equilibrium even at 0.1%/s. The faster director recovery is also reported in other studies[9], [10], [11], [12]. Moreover, at long-term relaxation, we found director continuously rotates over time because the viscous network extension further realigns the director. Using DIC, we can capture rate-dependent strain components under uniaxial tension. In particular, significant shear strain was observed induced by director rotation (Figure 1b). Intriguingly, when the angle between the initial director and tension direction is large enough, the shear strain non-monotonically changes with the stretch.
Besides experimental characterization, several viscoelastic models have been proposed to model the rate-dependent response [9], [11], [13], [14]. In particular, Zhang et al.[13] proposed a viscoelastic model that considers both the viscous network and director via a Kelvin-Voigt model. Wang et al.[14] developed a viscoelastic model assuming the multiplicative decomposition of the deformation gradient into elastic and viscous parts, and considering the viscous director rotation. To achieve better quantitative comparisons between theoretical predictions and experimental results, such as capturing the stress plateau of the semi-soft response, we recently proposed a viscoelastic constitutive model for LCEs based on the generalized Maxwell model. We phenomenologically modified the conventional semi-soft elastic energy, assuming the semi-soft parameter, describing the overall fluctuation of the director’s alignment, decreases with deformation[15]. We consider homogeneous deformation of LCE films with a tilted initial director subjected to uniaxial tension under different stretching rate 
(Figure 1b). The result shows that the director rotates towards the stretching direction, inducing a softening stress-strain response and large shear deformation (Figure 1c). As the stretching rate increases, the nominal stress s increases, while shear stretch 
and director 
rotation decrease. The predictions of our viscoelastic model agree overall well with our experiments. We then study the inhomogeneous deformation of a LCE film with an off-center hole using the finite element method (FEM) (Figure 1d). Our model is implemented in COMSOL and the COMSOL file will be made available together with the published paper. Figure 1d shows snapshots of the deformation of the film from both experiments and simulations under different applied stretches, along with the contours of the director distribution cosθ from the numerical simulations. Blue lines from the experiments and black lines from the simulations, in the X and Y directions in the reference states, are drawn for comparison. The overall deformation predictions agree well with the experimental results.
Figure 1(a)Schematics of the crossed-polarized optical measurement for directors, and the brightness changes of LCEs via rotating polarizers. (b) shear strain distribution using the DIC method. (c) Theoretical predictions for viscoelastic responses of LCEs under uniaxial tension compared with experimental results. Dependence of nominal stress, shear stretch and director rotation on external stretch under different stretching rates. (d) Experimental and numerical results of the deformation of a LCE with an off-center hole under various stretches. The color bar represents the director filed cosθ.
Anomalous inhomogeneous deformation
Due to the strong stress-director coupling, LCEs show anomalous inhomogeneous deformation compared to traditional elastomers. Here we introduce two study cases – inflation of a balloon and uniaxial stretching of a sheet with a center hole.
The soft behavior of LCEs distinguishes themselves from traditional neo-Hookean materials, leading to anomalous inflation of balloons and instabilities[16], [17], [18], [19]. He et al[16] reported that a balloon with its initial director in the axial direction exhibits rapid expansion in the radius direction under low pressure, driven by the rotation of mesogens (Figure 2a). As the pressure increases beyond a certain threshold, expansion occurs in both radius and axial direction. The inflation behavior changes subjected to axial load, leading to the formation of a bulge, which is accompanied by the shortening of the balloon’s length. Giudici et al[17] investigated the instabilities due to the rotation of the director (Figure 2b). Due to the spontaneous strain driven by the director, LCEs show unusual mechanics, i.e. sudden phase separation occurs when a LCE balloon is heated at a fixed volume, and conversely, a volume jump happens when it is cooled at a constant pressure. Lee et al[18] further demonstrated the soft behavior of LCEs lowers the critical pressure required for instability while amplifying the volume jump through the inflation of spherical and cylindrical balloons.
Our recent work[20] on the tension of a LCEs sheet with a center hole revealed an unusual distribution of stress and strain concentrations, distinct from those observed in neo-Hookean materials (Figure 2c). When the initial director is aligned with the tension direction, LCEs exhibit greater stress and strain concentrations compared to neo-Hookean materials, primarily due to the director rotation. Interestingly, at small applied strains, strain concentration does not coincide with stress concentration, showing two peaks; however, they become aligned as the applied strain becomes large. Peng et al.[21] further demonstrated that stress concentration varies with the different initial director, reaching a minimum when the initial director is oriented at 45° to the tension direction. These findings provide valuable insight into the mechanics of LCEs, with potential implications for their applications in responsive and programmable systems.
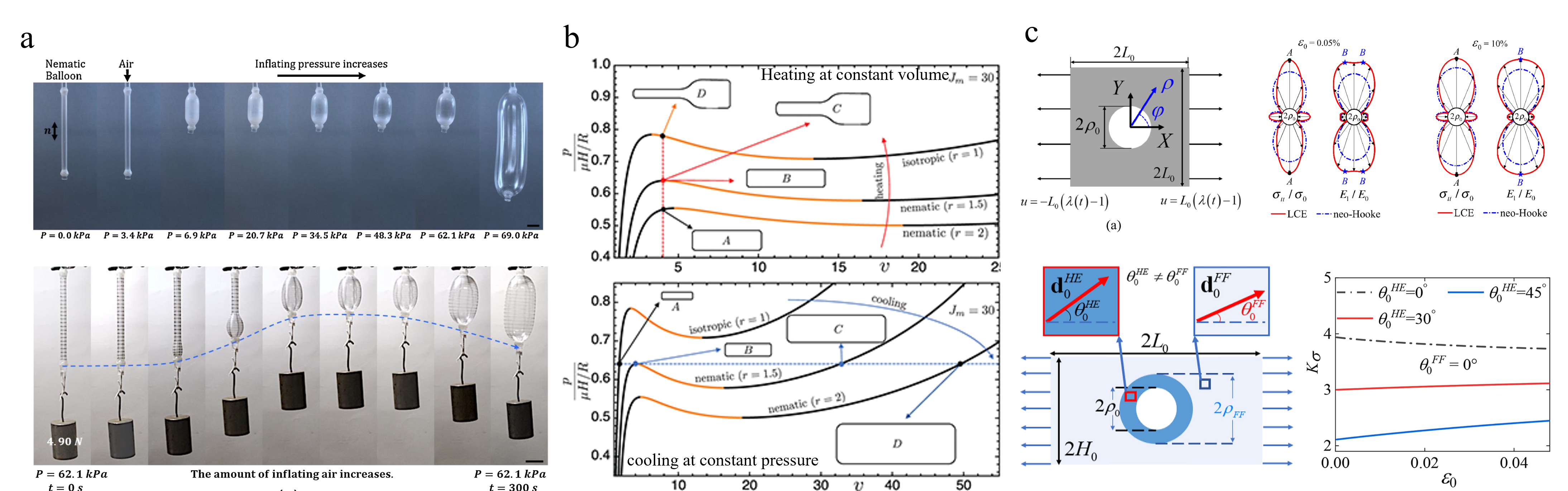
Figure 2(a) Inflation of a cylindrical balloon made of nematic LCEs[16]. (b) Gent pressure curve for an LCE ballon[17]. (c) Stress and strain concentration around the center hole in a LCEs sheet, and stress concentration with different initial director[20], [21].
Fracture behavior
Previous studies about fracture energy and stress concentrations indicated that the fracture behavior of LCEs could be quite different from that of neo-Hookean materials[22], [20], [21], [23], [24]. In this section, we will characterize the stress, strain, and director distribution around the crack tip, and report how stress-director coupling leads to exceptional fracture behavior[25] and subsequent unusual crack propagation.
We first study the stress, strain and director fields at the crack tip of an edge-cracked LCEs film with various initial directors (Figure 3a). From FEA, we found distinct stress and strain distributions in LCEs compared to traditional neo-Hookean materials (Figure 3b). When the initial director is parallel to the stretching, the stress and strain are symmetrical about the crack plane but show elliptical shapes. Conversely, when the initial director is tilled to the stretching direction, the stress and strain distributions become asymmetrical about the crack plane. Notably, the stress and strain concentrations at the crack tip are not coincident in LCEs caused by spontaneous strain. Through examining the director distribution by both FEA and optical polarization (Figure 3c), we observed the director rotate in opposite direction at a critical polar angle ϕ. For parallel loading, the director near the crack tip rotates clockwise at ϕ<0° and counter-clockwise at ϕ>0°, inducing symmetric spontaneous strain. In contrast, for tilted loading, significant director rotation occurs near the crack tip and a domain wall is observed along a critical polar angle, where the director rotates clockwise in the region with a larger polar angle and counter-clockwise in the region with a smaller polar angle, leading to asymmetrical stress/strain distribution and elliptical stress/strain contour lines with the smoothest gradient direction close to the critical polar angle.
To further assess the fracture behavior, we compared crack opening displacement and energy release rate – J-integral for LCEs with different directors with neo-Hookean materials (Figure 3d). In general, LCEs with the initial director tilted to the loading direction exhibit a much smaller crack opening and lower energy release rate than those in traditional neo-Hookean materials, while LCEs with parallel loading exhibit higher values. We attribute these findings to a combined effect of bulk softening at the remote region and the formation of domains of opposite director rotation near the crack tip.
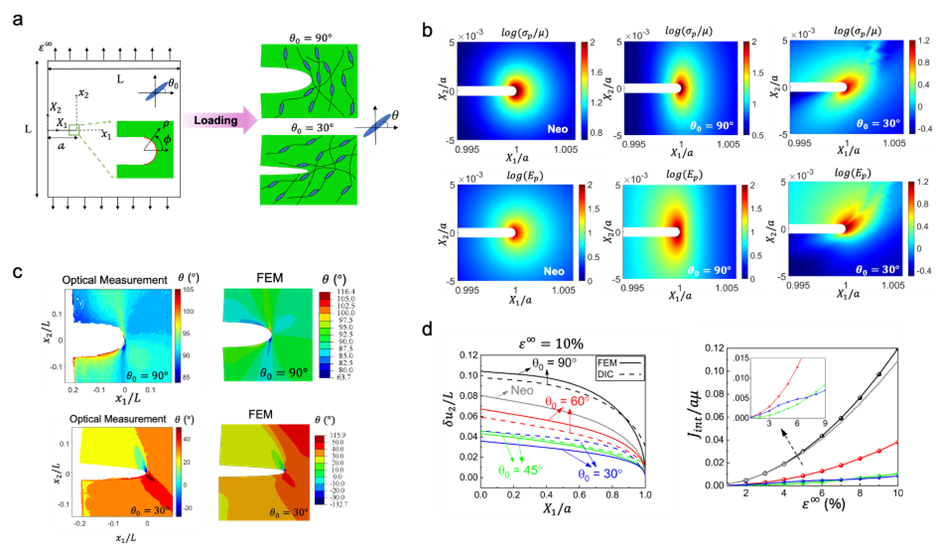
Figure 3 (a)Schematic of the LCEs film with edge crack. (b) Normalized principal stress (top) and strain (bottom) around the crack tip of a Neo-Hookean material, LCEs with θ0=90° and 30°. (c) Director distribution of LCEs with θ0=90° and 30°. (d) The crack opening displacement and normalized J-integral of a Neo-Hookean material and LCEs with varying initial director.[25]
Although the unique mechanical properties of LCEs, as discussed above, have been extensively studied, the fracture behavior of LCEs remains relatively unexplored, likely due to the complex director rotation involved. Only few studies have examined LCE fracture, primarily focusing on characterizing the crack-tip fields without crack propagation[25], and measuring fracture energy through pure shear tests[22], [23]. The crack propagation and failure criteria with respect to the director, stretching rate, and geometry of LCEs remain unresolved.
We combined experiments and phase-field fracture model to systematically study the fracture of monodomain LCEs[26]. We stretch edge-cracked monodomain LCE samples (Figure 4a), record their stress-stretch relations and crack paths with varying initial directors and stretching rates. The key assumption of our study is that cracks prefer to propagate perpendicular to the director of a LCE. Figure 4b-e show the experimental and simulation results of. Figure 4b-c show the deformation, fracture process, and the final fracture path of a LCE sample with a large length-to-width ratio. In both experiments and simulations, the horizontal lines drawn on the sample serve as visual references. As the stretch increases, the pre-crack opens asymmetrically, and the blue lines rotate, indicating substantial shear deformation. The crack propagates almost horizontally in the deformed configuration. After the sample is fully fractured and relaxed, the fracture path is tilted, which can be explained by the combined effect of the shear deformation and the almost vertical director at the crack tip due to the director-stress coupling (Figure 4d). Figure 4e shows numerical and experimental comparison of the stress-stretch responses for different stretching rates and initial directors. For a LCE with a lower length-to-width ratio, the fracture path shows an initial upward trajectory followed by a downward trend (Figure 4f). Figure 4g shows the director distribution in the early stage of the crack propagation, where the director in front of the crack tip is tilted, leading to the upward fracture path in the deformed configuration. Our model shows good overall predictions of the deformation, stress-stretch response, and fracture path of LCEs with different directors and geometry under different loading rates.
Figure 4 (a) Schematic of a LCE sample with a tilted initial director and a horizontal edged crack subjected to uniaxial tension. The initial director is illustrated by the orange ellipse. Images from (b) experiments and (c) simulations showing the deformation and crack propagation at different stretches, and the tilted fracture paths in the relaxed samples. The color bar represents the phase field d, and the material with d>0.95 has been removed. (d) Director distribution in front of the crack tip, where the color bar represents the x component of the director, cosθ. (e) Numerical and experimental stress-stretch responses for various initial directors and stretching rates. (f) Fractured samples under two stretching rates from the experiments and simulations. (g) Corresponding director distribution at λ=1.85
Summary
In this journal club, we discuss anomalous mechanics behavior of LCEs:
1. We present the rate-dependent stress, shear strain, and director rotation of LCEs. Furthermore, we developed a new viscoelastic model, by modifying the classical semi-soft model, to better capture the rate-dependent constitutive behavior of LCEs.
2. We present the anomalous inhomogeneous deformation due to the soft behavior induced by director rotation. Two cases – the inflation of a balloon and uniaxial stretching of a LCEs sheet with a center hole – were introduced.
3. We discuss the effect of stress-director coupling on the unique stress, strain and director distributions around the crack tip and the consequent crack propagation in LCEs with various initial directors.
The above studies provide guidance to design LCE materials and structures. More theoretical and experimental studies are needed to fully reveal the unique mechanical behavior, especially the fracture behavior, of LCEs.
Reference
[1] M. Warner and E. M. Terentjev, Liquid Crystal Elastomers. OUP Oxford, 2007.
[2] K. Urayama, R. Mashita, I. Kobayashi, and T. Takigawa, “Stretching-Induced Director Rotation in Thin Films of Liquid Crystal Elastomers with Homeotropic Alignment,” Macromolecules, vol. 40, no. 21, pp. 7665–7670, Oct. 2007, doi: 10.1021/ma071104y.
[3] Y. Xiao, J. Wu, and Y. Zhang, “Recent advances in the design, fabrication, actuation mechanisms and applications of liquid crystal elastomers,” Soft Sci., vol. 3, no. 2, p. 11, 2023, doi: 10.20517/ss.2023.03.
[4] A. Hotta and E. Terentjev, “Long-time stress relaxation in polyacrylate nematic liquid crystalline elastomers,” J. Phys.-Condens. Matter, vol. 13, pp. 11453–11464, Dec. 2001, doi: 10.1088/0953-8984/13/50/305.
[5] A. Azoug, V. Vasconcellos, J. Dooling, M. Saed, C. M. Yakacki, and T. D. Nguyen, “Viscoelasticity of the polydomain-monodomain transition in main-chain liquid crystal elastomers,” Polymer, vol. 98, pp. 165–171, Aug. 2016, doi: 10.1016/j.polymer.2016.06.022.
[6] M. Schönstein, W. Stille, and G. Strobl, “Effect of the network on the director fluctuations in a nematic side-group elastomer analysed by static and dynamic light scattering,” Eur. Phys. J. E, vol. 5, no. 5, pp. 511–517, Aug. 2001, doi: 10.1007/s101890170034.
[7] D. Mistry, P. B. Morgan, J. H. Clamp, and H. F. Gleeson, “New insights into the nature of semi-soft elasticity and ‘mechanical-Fréedericksz transitions’ in liquid crystal elastomers,” Soft Matter, vol. 14, no. 8, pp. 1301–1310, 2018, doi: 10.1039/C7SM02107K.
[8] J. Blaber, B. Adair, and A. Antoniou, “Ncorr: Open-Source 2D Digital Image Correlation Matlab Software,” Exp. Mech., vol. 55, no. 6, pp. 1105–1122, Jul. 2015, doi: 10.1007/s11340-015-0009-1.
[9] C. Wei, S. Cao, Y. Zhou, D. Lin, and L. Jin, “Rate-dependent stress-order coupling in main-chain liquid crystal elastomers,” Soft Matter, vol. 19, no. 41, pp. 7923–7936, 2023.
[10] C. Luo, C. Chung, C. M. Yakacki, K. Long, and K. Yu, “Real-Time Alignment and Reorientation of Polymer Chains in Liquid Crystal Elastomers,” ACS Appl. Mater. Interfaces, vol. 14, no. 1, pp. 1961–1972, Jan. 2022, doi: 10.1021/acsami.1c20082.
[11] C. Chung, C. Luo, C. M. Yakacki, B. Song, K. Long, and K. Yu, “Revealing the unusual rate-dependent mechanical behaviors of nematic liquid crystal elastomers,” Int. J. Solids Struct., vol. 292, p. 112712, Apr. 2024, doi: 10.1016/j.ijsolstr.2024.112712.
[12] A. Fukunaga, K. Urayama, T. Takigawa, A. DeSimone, and L. Teresi, “Dynamics of Electro-Opto-Mechanical Effects in Swollen Nematic Elastomers,” Macromolecules, vol. 41, no. 23, pp. 9389–9396, Dec. 2008, doi: 10.1021/ma801639j.
[13] Y. Zhang, C. Xuan, Y. Jiang, and Y. Huo, “Continuum mechanical modeling of liquid crystal elastomers as dissipative ordered solids,” J. Mech. Phys. Solids, vol. 126, pp. 285–303, May 2019, doi: 10.1016/j.jmps.2019.02.018.
[14] Z. Wang, A. El Hajj Chehade, S. Govindjee, and T. D. Nguyen, “A nonlinear viscoelasticity theory for nematic liquid crystal elastomers,” J. Mech. Phys. Solids, vol. 163, p. 104829, Jun. 2022, doi: 10.1016/j.jmps.2022.104829.
[15] Y. Zhou, C. Wei, and L. Jin, “A modified semi-soft model of liquid crystal elastomers: application to elastic and viscoelastic responses,” Under Revision., 2024.
[16] Q. He, Y. Zheng, Z. Wang, X. He, and S. Cai, “Anomalous inflation of a nematic balloon,” J. Mech. Phys. Solids, vol. 142, p. 104013, Sep. 2020, doi: 10.1016/j.jmps.2020.104013.
[17] A. Giudici and J. S. Biggins, “Giant deformations and soft-inflation in LCE balloons,” Europhys. Lett., vol. 132, no. 3, p. 36001, Dec. 2020, doi: 10.1209/0295-5075/132/36001.
[18] V. Lee and K. Bhattacharya, “Universal deformations of ideal liquid crystal elastomers,” Oct. 31, 2022, arXiv: arXiv:2210.17372. doi: 10.48550/arXiv.2210.17372.
[19] V. Lee and K. Bhattacharya, “Actuation of cylindrical nematic elastomer balloons,” J. Appl. Phys., vol. 129, no. 11, p. 114701, Mar. 2021, doi: 10.1063/5.0041288.
[20] Y. Jiang, L. Jin, and Y. Huo, “Unusual stress and strain concentration behaviors at the circular hole of a large monodomain liquid crystal elastomer sheet,” J. Mech. Phys. Solids, vol. 156, p. 104615, Nov. 2021, doi: 10.1016/j.jmps.2021.104615.
[21] Z. Peng, Y. Jiang, Y. Chen, and Y. Huo, “Attenuating liquid crystal elastomers’ stress concentration by programming initial orientation,” Int. J. Mech. Sci., vol. 249, p. 108274, Jul. 2023, doi: 10.1016/j.ijmecsci.2023.108274.
[22] W. Fan, Z. Wang, and S. Cai, “Rupture of Polydomain and Monodomain Liquid Crystal Elastomer,” Int. J. Appl. Mech., vol. 08, no. 07, p. 1640001, Oct. 2016, doi: 10.1142/S1758825116400019.
[23] R. Annapooranan and S. Cai, “Thermally induced self-rupture of a constrained liquid crystal elastomer,” Eng. Fract. Mech., vol. 269, p. 108584, Jun. 2022, doi: 10.1016/j.engfracmech.2022.108584.
[24] Y. Jiang, D. Li, Y. Chen, and Y. Huo, “Analysis of stress and strain concentration around a centralized elliptical hole in a monodomain liquid crystal elastomer sheet,” Int. J. Solids Struct., vol. 264, p. 112079, Mar. 2023, doi: 10.1016/j.ijsolstr.2022.112079.
[25] C. Wei, Y. Zhou, B. Hsu, and L. Jin, “Exceptional stress-director coupling at the crack tip of a liquid crystal elastomer,” J. Mech. Phys. Solids, vol. 183, p. 105522, 2024.
[26] Y. Zhou, C. Wei, and L. Jin, “Fracture of liquid crystal elastomers,” Submitted, 2024.